摘要

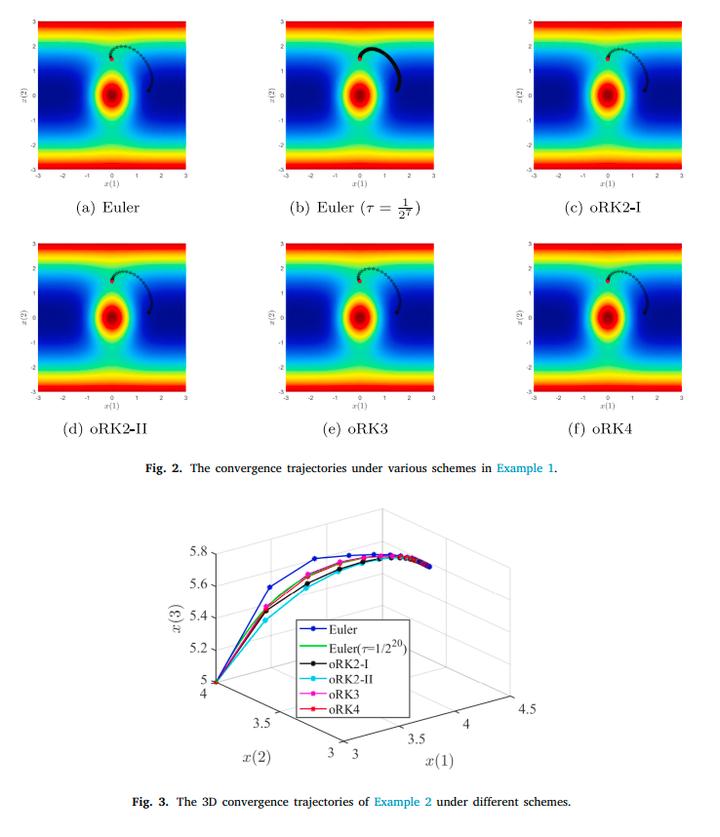
Saddle points are prevalent in complex systems and contain important information. The high-index saddle dynamics (HiSD) and the generalized HiSD (GHiSD) are two efficient approaches for determining saddle points of any index and for constructing the solution landscape. In this work, we first present an example to show that the orthonormality of directional vectors in saddle dynamics is critical in locating the saddle point. Then we construct two orthonormalized Runge-Kutta schemes tailored for the HiSD and GHiSD. We find that if a set of vectors are almost orthonormal with the error O(tau(alpha)) for some alpha>0, then the Gram-Schmidt process also applies an O(tau(alpha)) perturbation to orthonormalize them. We apply this and employ the structures of Runge-Kutta schemes to prove the almost orthonormality in numerical schemes and then prove their second-order accuracy with respect to the time step size. We substantiate the theoretical findings by several numerical experiments.